TEORÍA DE ERRORES Y ÁNGULOS INTERNOS Y EXTERNOS
El objetivo de esta temática es analizar los
posibles errores que se pueden cometer al realizar las mediciones, sus
orígenes, características, magnitudes, como se determinan, clasifican y
propagan. Con ello podremos calificar las medidas topográficas
y definir si son útiles conforme los objetivos de la tarea y las exigencias que
con ella se pretenda.
En los levamientos topográficos se determinan
medidas lineales y angulares que resultan de una medición directa con
instrumentos y en un gran número se obtienen de una determinación indirecta.
Es importante hacer notar que el término “error” no
tiene la acepción común de equivocación, sino que su significado es asimilable
a impresión, vacilación, imperfección o indeterminación.
Los errores propios de la medición provienen:
a) Del instrumental y accesorios usados en la
medición: ya que éstos pueden tener imperfecciones en sus partes, en el
ensamble de éstas. Asimismo las imperfecciones pueden ser de fabricación o
debido a su uso. Estos errores tienen la ventaja de poder corregirse o bien
compensarse mediante métodos de medición o sino calcular su influencia para
corregir las lecturas afectadas. Además todas las escalas de medición lineal y
angular tienen limitaciones que impone su menor división.
b) Del personal que la realiza: El operador al
medir depende de sus sentidos. La agudeza de la vista o sensibilidad del tacto
son los que intervienen con más frecuencia. Por su importancia y frecuencia se
cita: el centrado y calaje (al ubicar deficientemente el instrumento o sus
accesorios), la visación (por falta de una exacta coincidencia dentro del campo
del anteojo), la coincidencia de trazos, imágenes, bordes, etc., la apreciación
(al estimar fracciones, interpretarlas, interpolar), el redondeo (al suprimir
medidas por exceder las exigencias propias de la tarea. Cabe señalar que la
actuación personal se extiende a la elección de los procedimientos y métodos,
las tareas de cálculo y descripción final motivo del trabajo.
c) De las condiciones en que se realiza: Se
destacan las atmosféricas y del lugar. La atmósfera, el viento el sol, la
temperatura la humedad y presión son de suma importancia pues llegan a impedir
las tareas. Los parámetros de precisión, asimismo, se establecen para
condiciones favorables o desfavorables. Respecto del lugar en términos
generales, operar con comodidad y seguridad mejora los resultados. La
inestabilidad, la vegetación, cursos de agua, fango, relieve escarpado, etc.
dificultan las operaciones, particularmente los movimientos y la visibilidad.
TIPOS DE ERRORES
Previo a ello cabe aclarar que en muchos casos se cometen equivocaciones que las diferenciamos de los errores, en tanto y en cuanto las equivocaciones son “errores groseros” que tienden a ser relativamente grandes y fundamentalmente evitables; normalmente son yerros del operador/es provenientes de distracciones, descuidos, imprevisores, principios erróneos, a veces causados por negligencia, cansancio o hasta inadvertidamente usar datos o referencias equivocadas.
Errores sistemáticos
Básicamente son errores controlables que afectan las observaciones con una influencia constante o que responde a una ley determinada, por ello pueden ser identificados y controlados. Los constantes en general provienen de defectos instrumentales y causan errores hasta tanto no se los corrija mediante un ajuste mecánico, ej. Una cinta cuya longitud no es correcta: si en vez de 50m tiene 50.005m (puede ser originado en su fabricación y/o uso).
Los variables generados normalmente por diferentes condiciones operativas (temperatura, presión, humedad, etc.). Las causas más comunes de estos errores son: defectos instrumentales, diferentes condiciones operativas, características propias de los sentidos del operador, discrepancias provenientes de los métodos de medición y cálculo.
Errores accidentales
Son aquellos originados por causas fuera de control del operador y pueden provenir de tres factores: instrumental, personal y condiciones. Su manifestación es imprevisible, constituyendo un hecho azaroso, acotado por formas de prevención dispuestas por el operador al elegir instrumental, métodos, condiciones y un medio de estricto control del proceso de medición (de acuerdo a la precisión exigida). Estos errores imprevisibles, encasillados en lo eventual y fortuito constituyen hechos aleatorios y su magnitud y frecuencia se estudia a través de la Teoría de las probabilidades.
Su magnitud es tal que cuando más pequeños son, mayor es la probabilidad de cometerlos. Puede decirse que los errores pequeños son mas frecuentes que los grandes.
La probabilidad de cometer errores positivos y negativos es la misma, por ello los errores accidentales tienden a compensarse, lo que se acentúa en la medida que la serie tenga más observaciones.
Las tareas topográficas tiene impuestas tolerancias que son le límite del error a cometer o los máximos errores aceptables en mediciones y determinaciones. Se trata regularmente de un valor numérico resultante de expresiones o fórmulas empíricas establecidas por organismos de control, estatales o privados que tienen en cuenta distintas circunstancias que rodean la medición considerada.
Valor más probable
La teoría de errores, es una metodología que trata de llegar a disponer de un valor que represente “correctamente” esa medida, en base a una serie de observaciones (exentas de equivocaciones). Con medidas afectadas por errores accidentales se está en condiciones de buscar un “valor representativo” que además se utilizará como modelo para la comparación. Esta metodología es la aplicada habitualmente por el ser humano cuando define si “algo es lindo o feo”, “si está bien o mal”, .. lo hace en base a un modelo de referencia.
En nuestro caso la comparación se hace matemáticamente. Teniendo presente que el “valor exacto” de una magnitud es desconocido se utiliza la media aritmética de las medidas que integran la serie como el valor más probable, ya que por conceptos basados en principios estadísticos resulta el valor más representativo.
Así dada la serie compuesta por las observaciones: x1, x2, .. , xn entonces el valor más probable (M) será:
M= x1+x2+..+xn = Σ xi
Error Aparente y Error Verdadero
Determinar el error es comparar la “medida” con otro valor que sirve de modelo (Error= medida – valor modelo).
Si ese valor modelo es el valor más probable (a falta de un valor verdadero), entonces podemos determinar el error aparente (V).
V= xi – M
Vale tener presente que: la media aritmética hace nula la sumatoria de los errores aparentes.
A diferencia del error aparente, si la comparación se realiza con el “valor verdadero” (X), entonces estamos obteniendo el error verdadero (e) .
e=xi – X
Error relativo (Vr)
A menudo en la práctica topográfica se compara el valor absoluto del error aparente con la media aritmética, de este cociente se puede observar la bondad técnica de un valor.
Vr = IVI
M
Ej. si al medir 300m se tiene un error aparente de 6 cm, entonces:
Vr= 6/30000 = 1/5000
si al medir 300m se tiene un error aparente de 20 cm, entonces:
Vr= 20/30000 = 1/1500
Es habitual también expresar el error relativo en forma porcentual.
Precisión
Con éste término expresamos el grado de refinamiento o perfección aplicado a una medición, asociado a la calidad de su ejecución.Las mediciones de una serie con gran homogeneidad (poca dispersión) implican una precisión alta. Esto no es sinónimo de exactitud, ya que por ejemplo ante un error sistemático podemos estar en presencia de precisión y no exactitud.
Así podemos hablar de la magnitud de los errores, que nos van a expresar el entorno o límites. Es así habitual expresar los valores numéricos asociado a este límite a modo de expresar una medida en forma técnicamente correcta y completa.
Existen distintas maneras de expresar las medidas de precisión. Las mas utilizadas en topografía son:
- Error promedio (µ)
- Error probable (p)
- Error Medio cuadrático (m)
1. El error promedio es la media aritmética de los valores absolutos de los errores aparentes.
2. El error probable se lo define como el valor ubicado en el medio del conjunto de los valores absolutos de los errores aparentes.
3. Al error medio cuadrático se lo identifica también como la desviación estándar muestral y se puede expresar en función de los errores verdaderos o de los errores aparentes.
ÁNGULOS INTERNOS Y EXTERNOS
Determinar ángulos internos
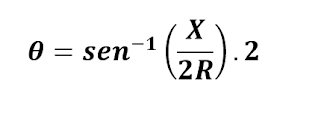
Los ángulos internos y externos se representan en grados, minutos y segundos.
Error de ángulos


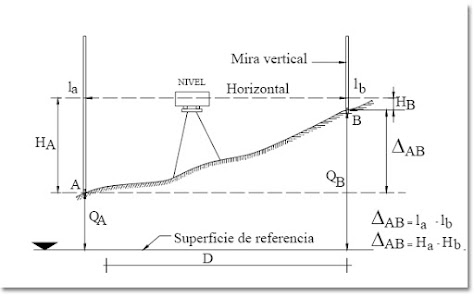


Comentarios
Publicar un comentario